|
Y.V. Solodyannikov
Elements of mathematical modeling and identification of blood circulation system
Computer medicine
Program
Recently in biology and medicine there was expressed the tendency to application of
exact mathematical methods and resources of computer facilities for research of the processes occuring in organism of the person and, in particular, in
his main physiological system - in system of blood circulation (BC). In this connection special interest represents digital simulation of processes of
regulation and handle in BC, creation of mathematical applications and software oriented to problem solving of artificial and auxiliary blood circulation. Models of BC are usually divided into two main groups: models
of hemodynamics of the cardiovascular system; models of regulation of intimate ejection.
Models of hemodynamics reflect processes in separate areas (for example, in large vessels) of BC. They are created, as a rule, either on the basis of direct analogy to electrical chains, or using
indirect analogy of solution of the model equations with the help of the computer. Models of Shumakov (with co-authors), Defares, for example, can be related to as models of the first group
Models of the second group consider main characteristics and features of heart such as pump, vascular system and control curcuit. As a rule, these models are described by a system of equations with
concentrated parameters. In their turn, models of this group can be divided into opened and closed. Opened models are the models of Amosov (with co-authors), Grigoryan. In closed models the most interest is drawn to works of Topam and Warner, Pickering (with co-authors), Grodins
(with co-authors), Jeins and Carson, Palets, Beneken, Moller, Guyton, as well as to the model of Shumakov (with co-authors) referencing to the problem of artificial and auxiliary blood circulation.
Numerous researches of response of the cardiovascular system on physical load were carried on. Models of BC were used for studing of various pathological states, such as intimate unsufficiency,
hypoxia, hypertonic illness, blockade of baroreceptors, change of volume of circulating blood in BC,etc.
Models of small circle of blood circulation (Palets and Bushnaja, Hymen) are known. The mathematical model of six-chamber heart is intended for research on dinamics of heart cameras interaction, including ears of the auricle.
Large models of common regulation of BC, represent the complex structure of cooperating and intersected circuits, they model levels of organization, starting from the lowest and up to the
supreme(nervous).
The number of works is known in which methods of the theory of automatic control are used for learning regulation of blood circulation. In these models, as a rule, a controlled variable is arterial or sistolic pressure or minute volume of blood. Models
of BC are successfully applied to identification of system parameters on measurements of input and output.
In this specific work the class of regulation of intimate ejection models is observed.
The basis for their development is the model offered by V.I. Shumakov, academician of AMS, and professor G.P.Itkin, Dr.Sci.Med. Description of the
model is given from their agreement. Key feature of the given class of models is that they allow studing the oscillatory (in particular, periodic) processes in BC, unlike models of the averaged characteristics. These models
are self-tuning, that reflects major features of BC.
The system of blood circulation is represented by dinamic system of differential equations in classification of Neimark:
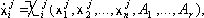 (1) (1)
where
i = 1,2,...,n ( n - order of the system ),
j = 1,2,...,l ( l - number of the different system definitions ),
A1,...,Ar - parameters, r - dimension of space of parameters,
Xij- - some nonlinear functions describing BC on various phases.
Transition from the description of the system number p to the description of the system number q (p, q are included in
the set of {1,2..., l}) in equations (1) occurs if the following equalities take place:
Spq(xp1,...xpn,t,k1,...,km) = 0, (2)
где
t -время,
k1,..., km - transition parameters, m- dimension of space transition parameters.
In moment tpqof transition from the description of the system number p to the description of the system number q (let's call it p-q-transition) values of new variables x1q,...,xnq are expressed through values of old variables
x1p,...,xnp according to the equations of sliding movements:
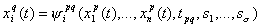 (3) (3)
i=1,2,.. ,n
s1,..,ss - a parameters of the slide.
Wewill remark, that considered system of differential equations is not autonomous, for as the variable t obviously enters the conditions of transition (2). The informative description of models will be given in chapter 1.There also will be given the results of digital simulation which have shown the good consent with the physiological data. Existence of
periodic movement of dinamic systen (DS) is proved either experimentally by numerical simulation on the computer, or analytically, depending on the type of functions. In case of non-linear functions analytical solution of a question on existence of periodic movements becomes rather complicated, in chapters 2 and 3 such proofs are given for two modifications of model (1) - (3) using method of the small parameter. The analysis of stability of stationary movements of DS allows to state the fact of model reality for as real BC has stationary steady movements, character and ranges of their stability are known from experiments. Besides, research of stability is necessary for the analysis of control systems in devices of artificial or auxiliary blood circulation, for research onintra-aortic counterpulsation, etc. Stability of isolated stationary movement of DS is understood in the sense of Lyapunov, and system research by means of analytical methods in general case of equations (1) - (3) is rather difficult. Therefore the work offers the research of stability which is carried only for the elementary system of the given class (in chapter 2). For a common case we have developed algorithm and the computer program on the basis of the numerical analysis of dot mappings of some surfaces without contacting DS.
Questions of identification the real BC by some model of class (1)-(3) are considered in chapter 5. While in the process of identification of BC, vector
y*(t) = j(A*, х*(t)), (4)
>depending on unknown parameters, is accessible to measurement. The task of identification of parameters of the system of blood circulation on measurements (4), taken from a real organism, is put as the task of definition of parameters A of models (1) - (3) (and sometimes in addition also parameters K and S), that give the least distance between y * (t) and appropriate variables
y(t) =j(A, x(t)). (5)
Thus it is considered, that the structure of model and the object coincide. Identification of parameters was carried out by various methods: the method of adaptive identification offered by A.A.Krasovskii, method of direct search, gradient methods, method of the least squares for the adapted basis and other. Results of comparison are given in chapter 5.
The requirement of identity, as a rule, is global and is not settled by identity in one given mode (solution of the system on the fixed entry
conditions and parameters). By the carried machine experiments it was shown, that in system (1) - (3) there are modes with multisemantic identification of several parameters. Therefore before identification it is necessary to solve the task of identifiability of DS in the given mode with the given measures (4), (5) or the task of choice of measures on which identification was
identification as a whole.
Let Y - be a set of graphs y(t) vector-function (5), G - set of initial conditions for (1) coordinate n-measured space Rn , A - set of parameters А. For analysis of observation in separate mode, full observation and identification of the system (1)-(5) there were designed methods and algorithms of the biaction check of images Y->G, Y->A by means of calculation of the rank of specially organized matrixes ( in chapter 4). Corresponding examples and results of the analysis of the system (1)-(5) are
given, too.
Variable identification stating DS conditions in (1) - (3) in the given research is considered in a context of the least squares method for the adapted basis of identification of parameters and states (chapter 4), and also on a basis Kalman filtering (chapter 5).
Present book is considered for the broad audience of readers among physicians, physiologists, physiologists-investigators, engineers, mathematicians, programmers.
One can object, saying that I try to connect unjoinable. However I have a deep belief, that exactly this approach is capable to give the best results in making methods of modeling and identifications of blood circulation most efficient, and it will definetely bring better understanding of each other to different specialists.
|