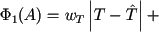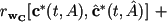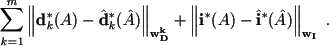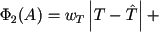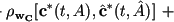Identification > Estimation criteria

For an arbitrary vector y of dimension N we define its weighted norm

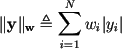with the vector of weights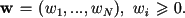

For an arbitrary integrable on the interval 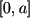vector-function 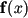and arbitrary integrable on an interval 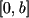vector-function 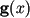we define the integral distance between them

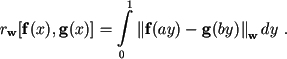For arbitrary continuous on the interval 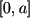vector-function 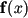and arbitrary continuous on the interval 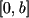vector-function 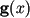we define the minimax distance between them

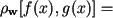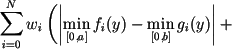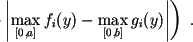Also introduce the following notation:

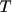	- duration of the cardiac cycle in the model,
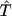	- duration of the cardiac cycle in the measurements of the object,
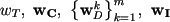	- system of weights, some empirical,
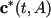	- model measurements, measuring paradigm C,
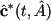	- object measurements, measuring paradigm C,
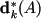	- model measurements, measuring paradigm D,
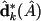	- object measurements, measuring paradigm D,
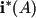	- model measurements, measuring paradigm I,
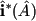	- object measurements, measuring paradigm I.

In the identification algorithm was implemented the following criteria for evaluating the deviations of measurements from the measurement model facility, as options for optimizing the functional (62).

• Integrated criterion. The distance is calculated as the integral of the weighted norms of the difference between the values measured in one cardiac cycle

  (63)

• Minimax criterion. The distance is calculated as the sum of deviations of measurements in the critical points of maximum and minimum of one cardiac cycle

  (64)

Identification > Estimation criteria