|
Ю.В.Солодянников
Элементы математического моделирования и идентификации системы кровообращения
Введение
Компьютерная медицина
Программа
В последнее время в биологии и медицине ярко выразилась тенденция к применению точных математических методов и средств вычислительной техники для исследования процессов, происходящих в организме человека и, в частности, в его основной физиологической системе - системе кровообращения (СК). В этой связи особый интерес представляет цифровое моделирование процессов регулирования и управления в СК, создание математического и программного обеспечёния, ориентированного на решение задач искусственного и вспомогательного кровообращения.
Модели СК обычно делят на две основные группы:
- модели гемодинамики сердечно-сосудистой системы;
- модели регуляции сердечного выброса.
Модели гемодинамики отражают процессы в отдельных участках (например, в крупных сосудах) СК. Они строятся, как правило, на основе прямой аналогии с электрическими цепями, либо косвенной аналогии при решении уравнений модели с использованием ЭВМ. К моделям 1-ой группы можно отнести, например, модели Шумакова с соавт., Дефареса.
Модели регуляции сердечного выброса рассматривают основные свойства и характеристики сердца как насоса, сосудистой системы и контуров управления., Эти модели описываются, как правило, системами уравнений с сосредоточенными параметрами. Модели 2-ой группы можно разбить на разомкнутые и замкнутые. К разомкнутым моделям можно отнести модели Амосова с соавт., Григоряна. Наибольший интерес среди замкнутых моделей представляют модели Топам и Уорнера, Пикеринга с соавт., Гродинза с соавт., Джейнса.и Карсона, Палеца, Бенекена, Меллера, Гайтона, а также модели Шумакова с соавт. применительно к задачам искусственного и вспомогательного кровообращения.
С помощью моделирования велись многочисленные исследования реакции сердечно-сосудистой системы на физическую нагрузку. Модели СК использовались при изучении различных патологических состояний, таких, как сердечная недостаточность, гипоксия, гипертоническая болезнь, блокада барорецепторов, изменение объема циркулирующей крови в СК и т.п. Известны модели малого круга кровообращения (Палец и Бушная, Хьюмен). Математическая модель шестикамерного сердца предназначена для исследования динамики взаимодействия камер сердца, включая ушки предсердия.
Большие модели общей, регуляции СК, представляют собой сложную структуру взаимодействующих и пересекающихся контуров, которые моделируют уровни организации, начиная от низших и до высших (нервных).
Известен ряд работ, в которых для изучения регуляции кровообращения используются методы теории автоматического управления. В этих моделях, как правило, управляемой переменной является артериальное или систолическое давление либо минутный объём крови.
Модели СК успешно применяются для определения (идентификации) параметров системы по измерениям входа и выхода.В настоящей работе рассматривается класс моделей регуляции сердечного выброса. Основой для их разработки служит модель, предложенная академиком АМН Шумаковым В.И. и д.м.н., профессором Иткиным Г. П., описание модели приведено с их согласия. Главной особенностью данного класса моделей является то, что они позволяют изучать (моделировать) колебательные (в частности, периодические) процессы в СК, в отличие от моделей усредненных характеристик. Эти модели являются самонастраивающимися (гомеостатическими), что отражает важнейшие свойства СК.
Система кровообращения представляется динамической системой (ДС) класса ДУ по классификации Неймарка:
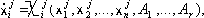 (1) (1)
где
i=1,2,..,n (n-порядок системы),
j=l,2...,l (l-число различных описаний системы),
A1,...Ar - параметры , r-размерность пространства параметров,
Xij- некоторые нелинейные функции, описывающие СК на различных фазах.
Переход от описания р-й системой к описанию q-й системой (p,q 1,2,...,l}) уравнений (1) происходит при выполнении равенств:
Spq(xp1,...xpn,t,k1,...,km) = 0, (2)
где
t -время,
k1,..., km - переходные параметры, m- размерность пространства переходных параметров.
В момент tpq перехода от описания р-й системой к описанию q-й системой (р-q-переход) значения новых переменных xq1,...,xqn выражаются через значения старых переменных xp1,...,xpn согласно уравнений скользящих движений:
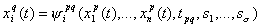 (3) (3)
i=1,2,.. ,n
s1,..,ss - параметры скольжения.
Заметим, что рассматриваемая ДС неавтономна, поскольку в условия перехода (2) явно входит переменная t.Содержательное описание моделей будет дано в гл.1. Там же - приведены результаты цифрового моделирования, которые показали хорошее согласие с физиологическими данными.
Существование периодического движения ДС доказывается либо экспериментально численным моделированием на ЭВМ, либо аналитически, в зависимости от вида функций Xji, Spq, Yipq. В случае, если эти функции нелинейны, аналитическое решение вопроса о существовании периодических движений затруднительно, в гл.2 и 3 такие доказательства приведены для двух модификаций модели (1)-(3) методом малого параметра.
Анализ устойчивости стационарных движений ДС позволяет установить факт реальности модели, поскольку реальная СК имеет стационарные устойчивые движения и из экспериментов известны характер и диапазоны их устойчивости. Кроме того, исследование устойчивости необходимо при анализе систем управления в аппаратах искусственного или вспомогательного кровообращения, при исследовании режимов внутриаортальной контрпульсации и т.д. Устойчивость изолированного стационарного движения ДС понимается в смысле Ляпунова, ее исследование аналитическими методами в общем случае уравнений (1)-(3) затруднительно. Поэтому в данной работе исследование устойчивости проведено лишь для простейшей системы данного класса (гл.2). Для общего случая нами были разработаны алгоритм и программа для ЭВМ на основе численного анализа точечных отображений некоторых поверхностей без контакта ДС.
Вопросы идентификации реальной СК некоторой моделью класса (1)-(3) рассматриваются в гл.5. В процессе идентификации СК измерению доступен вектор
y*(t) = j(A*, х*(t)), (4)
зависящий от неизвестных параметров. Задача идентификации параметров системы кровообращения по измерениям (4), снимаемым с реального организма, ставится как задача определения параметров А модели (1) - (3) (а иногда дополнительно еще и параметров К и S), дающих наименьшее расстояние между y*(t) и соответствующими переменными
y(t) =j(A, x(t)). (5)
При этом считается, что структура модели и объекта совпадают. Идентификация параметров проводилась различными методами: методом адаптивной идентификации, предложенным А.А.Красовским, методом прямого поиска, градиентными методами, методом наименьших квадратов по приспособленному базису и другими. Результаты их сравнения даны в главе 5.
Требование идентичности, как правило, является глобальным и не исчерпывается идентичностью в одном заданном режиме (решение системы с фиксированными начальными условиями и параметрами). Проведенными машинными экспериментами было показано, что в системе (1)-(3) существуют режимы с неоднозначной идентификацией никоторых параметров. Поэтому перед проведением идентификации необходимо решить задачу идентифицируемости ДС в заданном режиме с заданной системой измерений (4), (5) либо задачу выбора системы измерений, на которых идентификация была бы идентификацией в целом.
Пусть Y - множество графиков y(t) вектор-функций (5), G - множество начальных условий для (1) в координатном n-мерном пространстве Rn , A - множество
параметров А. Для анализа наблюдаемости в отдельных режимах, глобальной (полной) наблюдаемости и идентифицируемости системы (1)-(5) разработаны методы и алгоритмы проверки биективности отображений Y->G, Y->A с помощью расчета ранга специально организованных матриц (гл.4). Приведены соответствующие примеры и результаты анализа системы (1)-(5).
Идентификация переменных состояния ДС (1)-(3) в данной работе рассмотрена в контексте метода наименьших квадратов по приспособленному базису идентификации параметров и состояний (гл.4), а также на основе калмановской фильтрации(гл.5).
Настоящая книга рассчитана на широкий круг читателей- медиков, физиологов, физиологов-исследователей, инженеров, математиков, программистов. Мне могут возразить, что я пытаюсь соединить несоединимое. Однако у меня есть глубокое убеждение, что именно этот подход способен дать наилучшие результаты в создании эффективных методов моделирования и идентификации кровообращения, лучше понять друг друга различным специалистам.
| В работе над рукописью мне большую помощь оказали И.В.Гриневич, А.П.Прошин, Т.И.Сторожева, и я рад выразить им свою благодарность. Кроме того, мне хотелось бы выразить благодарность директору НИЦ самарского медицинского института им. Д.И.Ульянова профессору Бабкину С.M. и его сотрудникам в экспериментальной апробации программно-аппаратного комплекса идентификации системы кровообращения.
|
|