Mathematical model > Model of cardiac output regulation

The system of correlations (12) - (19) given here is a basis of our blood circulation model. These correlations are represented as an original formalization of Frank-Starling's heart law and describe the heart as a nonlinear oscillatory system.

The heart in our mathematical model is considered as a pump. The most important pump characteristics are: the values of systolic ventricular pressure P_i, cardiac cycle duration T and output ventricular volumes v_i.

Let us designate {τⁿ}, n = 0,1,... - the moments sequence of cardiac cycle beginning (the beginning of ventricular systole), Tⁿ = τⁿ - τ^n-1 - sequence of cardiac cycle durations .
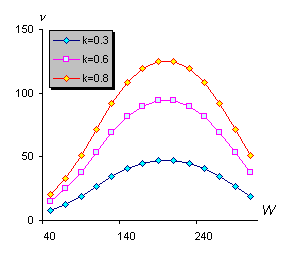
Let us write down correlations for Frank-Starling's heart law [15], that evaluates a dependence of ventricular output v_i from its filling at the start moment of heart compression cycle (enddiastolic volume) W_i:

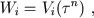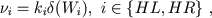(12)

where values k_i are named as ventricular inotropic factors, bell-kind function

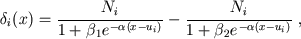(12.1)

where values N_i, u_i, α, β₁, β₂ are approximation constants and selected experimentally.

Chart

The dependence of ventricular output from ventricular enddiastolic volume for the different values of inotropic factor

For inotropic factor we have a dependence (54) from inotropic condition k_i and neurohumoral factor γ.

The correlations, similar to (12) , written separately for left and right ventricles, are given in the works of Amosov N. M. with co-authors [12]. Equations for ventricular output (12) are used in our model for definition of systole-diastole jump conditions (1-2-jump). As the ventricular output volume is determined as a difference between enddiastolic and endsystolic volumes, endsystolic ventricular volume w_iⁿ from (12) is defined as

(13)

whence 1-2-jump conditions in cardiac n-cycle are determined by correlations

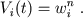(14)

In our model the cardiac cycle duration СК is defined as a value, reciprocally proportional to the value of neurohumoral factor γ in the moment of previous cycle ending

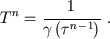(15)

Correlations (15) are used for definition of systole-diastole jump conditions (2-1-jump)

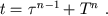(16)

The necessary value of ventricular output is provided with control by the value of average systolic ventricular pressure P_i . This control is in turn provided with a principle of negative feedback on misalignment between actual and nominal systolic duration. Nominal duration of ventricular systole  θ_iⁿ in the work [12] is determined through inotropic ventricular factor k_i by this formula

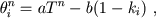(17)

where a, b – empirical constants of an approximation .
Actual systolic duration σ_iⁿ is determined as a moment of equality (14) execution . Misalignment between actual and nominal systolic duration in n-cycle

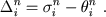(18)

In our model the value of average systolic ventricular pressure P_iⁿ⁺¹ in n+1-cycle is defined through the value of average systolic pressure P_iⁿ in n-cycle by a recursive ratio

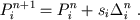(19)

Equation (19) claims, that average systolic ventricular pressure is constant during each systoleу. Under transition to the following cardiac cycle it is recalculated according to (19). The equation sets the control algorithm of systolic ventricular pressure depending on the value Δ_iⁿ and factors of sensitivity s_i . In the work [9] the important role of values s_i for existence and periodic movement stability of dynamic system (1) is given .

---

Mathematical model > Model of cardiac output regulation

References on the topic:

Mathematical model > Ventricular model

© Samara-Dialog Ltd. 2004-2009