Mathematical model > Classification

The building basis of the model is a class of models suggested in [9]. The main feature of this class - research and modelling of oscillatory and periodical processes in the modelling object. Our model is self-adapted, it reflects the most important homeostatic [7] features of the blood circulation system.

In outlook the model of this class is represented as a dynamic system

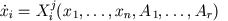(1)

where

i= 1,…,n ( n – system dimension),

j = 1,…,l (l– total number of system descriptions),

A = (A₁,…,A_r) – vector of parametres with dimension r,

some nonlinear functions X_i^j describe an object in different phases of cardiac cycle. The jump from p- description to q-description

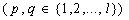
of equations system (1) takes place after satisfaction of p-q-jump conditions

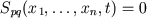(2)

In the moment of jump t_pq new values of condition variables are calculated through the values of old condition variables by means of sliding movement equations

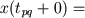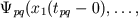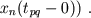(3)

The dynamic system describing with (1) - (3) is non-autonomy, because time variable t is included in jump conditions (2). The satisfaction of p-q-jumps means, that the modelling object is being described by different systems of differential equations in different phases of cardiac cycle (systole, diastole) .