Mathematical model > Ventricular model

1. Blood flow model.

The model of ventricles filling in diastolic phase and their evacuation in a systole is considered. Differential equations for ventricular blood volume are defined by the formula (9)

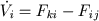(9)

where F_ki - blood flow through input valve, F_ij - blood flow through output valve. For left ventricle (i = HL) k = VR (pulmonary vein), j = AL (aorta), input valve - mitral, output valve - aortic. For right ventricle (i = HR) k = VL (venae cavae), j = AR (pulmonary artery), input valve - tricupsid, output valve - pulmonary.

Blood flow through output valve is determined by the difference between ventricular pressure P_i and arterial pressure P_j :

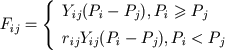(20)

The second part of the formula (20) describes a process of regurgitation in output valve in a diastolic phase in case of defect of valve locking element (valvular heart defect). In case of defect 0<r_ij<1, in norm r_ij=0.

Blood flow through input valve is determined by the difference between venous pressure P_k and ventricular pressure P_i:

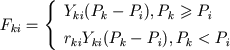(21)

The second part of the formula (21) describes a process of regurgitation in input valve in a diastolic phase in case of defect of valve locking element (valvular heart defect). In case of defect 0<r_ki<1, in norm r_ki=0.

Systolic ventricular pressure is determined according to (19). The ventricular model ends with the description of their diastolic filling. Systolic ventricular pressure is evaluated as a partial sum of Taylor's series of function decomposition of ventricular blood volume variable V_i :

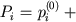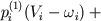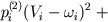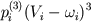(22)

where ω_i - stressless ventricular volume.

During the implementation of real model the function (22) is selected so that heart work could reflect the basic self-regulation laws and provide curves similarity of ventricular pressure.

2. Model of inotropism.

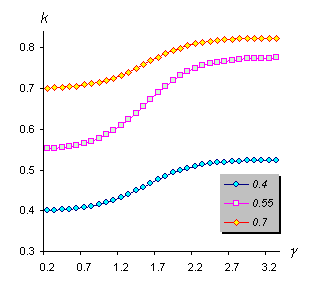
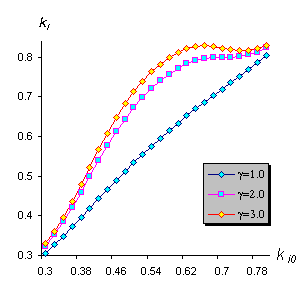
The major characteristic of pump ventricular function in our model is inotropic factor k_i. This numerical inotropic characteristic (contractility) of myocardium was defined in works of N.M.Amosov and co-authors [12], [18]. The main point of our results interpretation of these works is that inotropic ventricular factor is evaluated by the function of two variables - inotropic ventricular condition k_i0 and neurohumoral factor γ:

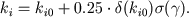(54)

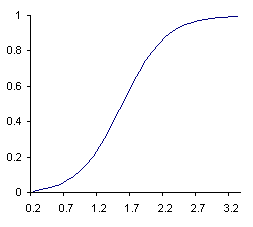
Sigmoid function of sympathetic inotropic sensitivity of myocardium describes the dependence of inotropic factor from neurohumoral factor:

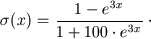(55)

Chart

Function of myocardial sympathetic inotropic sensitivity

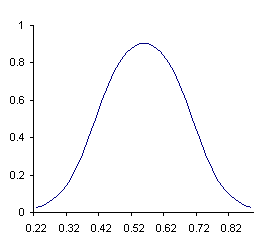
Bell-kind function of myocardial adaptable ability describes the level of neurohumoral factor on the value of inotropic factor depending on a base myocardial functional status (of inotropic status k_i0):

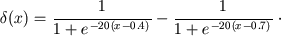(56)

Chart

Function of myocardial adaptable ability

Myocardial inotropism (contractility) in many cases is the main factor determining the value of cardiac output. Myocardial reduction ability is in turn determined by following factors.

1. Activity of sympathetic nervous system.
2. Heartbeat frequency.
3. Some pathological statuses with negative inotropic action (hypoxemia, acidosis, hypercapnia, myocardial ischemia, myocarditis etc.).
4. Myocardial mass. Its reduction under myocardial ischemia, myocardial infarction, cardiosclerosis leeds to decrease of reduction ability.
5. Drugs with inotropic action: negative (β-blockers, procainamide hydrochloride, quinidine, barbiturates and others) or positive (noradrenaline and its derivations, cardiac glycosides and others) .

In the formula (54) factors 1-2 are incarnated by the function of myocardial sympathetic inotropic sensitivity (55), and factors 3-5 by inotropic ventricular condition k_i0 and function of myocardial adaptable ability (56).

Chart

Dependence of inotropic factor from neurohumoral factor under different values of inotropic status ki0=0.4, ki0=0.55, ki0=0.7

Inotropic status k_i0 characterizes ventricular ability to throw more blood volume in vessels without increase of enddiastolic volume (i.e. without use of Frank-Starling's law), or the ability to throw the equal volume under more pressure in great vessels. It means, that under the same values of enddiastolic volume ventricles can extend their power. Under decrease of inotropic function (decrease of contractility) myocardial tension (increase of enddiastolic volume) does not cause the increase of myocardial power.

Chart

Dependence of inotropic factor from inotropic status under different values of neurohumoral factor

Mathematical model > Ventricular model